Sztywność pali w zależności od lokalizacji w fundamencie
Sztywność pali fundamentowych, a zatem także wartości sił przekrojowych w palach uzależnione są od wzajemnego rozstawu pali oraz ich umiejscowienia w fundamencie. W programie PaleKx zastosowano tzw. schemat fundamentu palowego, który umożliwia wykonanie obliczeń sił przekrojowych w palach jednocześnie dla kilku kierunków działania obciążenia poziomego oraz dla różnych rozstawów pali.
Przedstawiony poniżej schemat fundamentu palowego umożliwia odwzorowanie rzeczywistego układu pali w projektowanym fundamencie. Schemat składa się z dziewięciu charakterystycznych pali: narożnych (1, 3, 7, 9), krawędziowych (2, 4, 6, 8) i pala wewnętrznego (5).
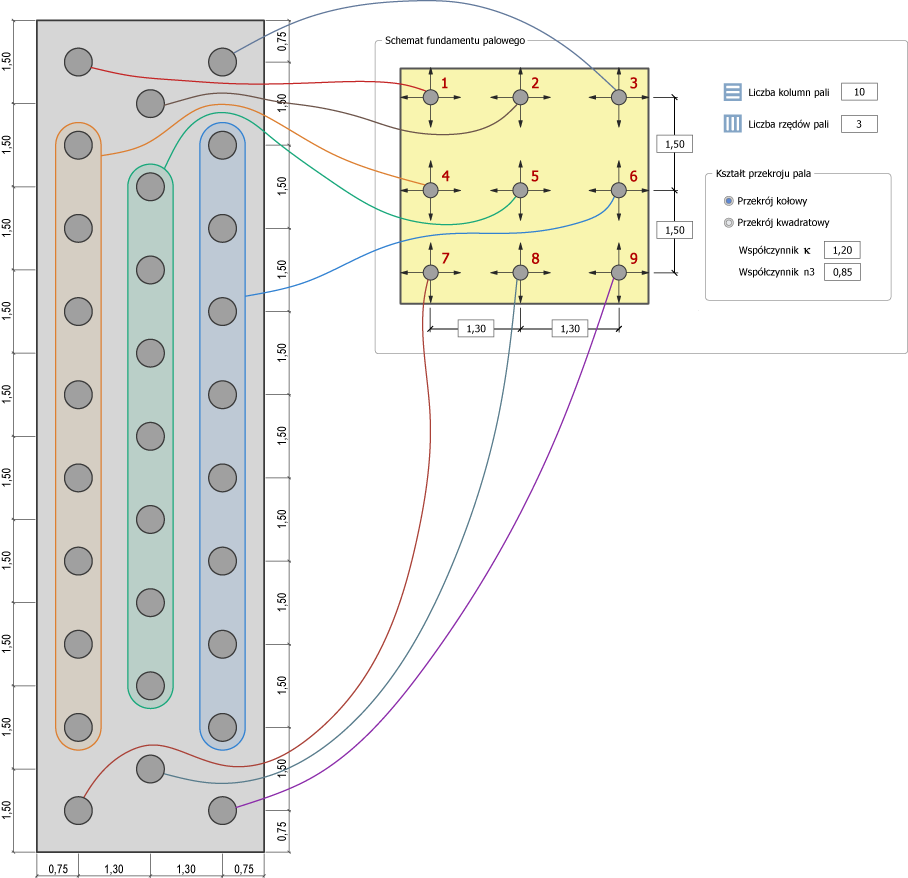
Charakterystyczne pale schematu fundamentu:
- Pal nr 5
Pal zlokalizowany w wewnętrznym rzędzie i wewnętrznej kolumnie pali. Jest ograniczony palami sąsiednich rzędów i sąsiednich kolumn – tzw. pal wewnętrzny grupy palowej, w którym powstają największe siły przekrojowe.
- Pal nr 2 i 8
Pale zlokalizowane w wewnętrznej kolumnie i skrajnym rzędzie pali. Są ograniczone palami sąsiednich kolumn lecz znajdują się w skrajnym rzędzie grupy palowej – tzw. pale krawędziowe.
- Pal nr 4 i 6
Pale zlokalizowane w wewnętrznym rzędzie i skrajnej kolumnie pali. Są ograniczone palami sąsiednich rzędów lecz znajdują się w skrajnej kolumnie grupy palowej – tzw. pale krawędziowe.
- Pal nr 1, 3, 7, 9
Pale zlokalizowane w skrajnym rzędzie i skrajnej kolumnie pali. Pale nr 1, 3, 7 i 9 nie są ograniczone palami sąsiednich rzędów ani sąsiednich kolumn grupy palowej – tzw. pale narożne, w którym powstają najmniejsze siły przekrojowe.
Zmienność modułu sztywności Kx oraz odporu bocznego Qxgr
Wartości modułu sztywności poziomej gruntu Kx oraz granicznego odporu bocznego gruntu Qxgr wpływają bezpośrednio na siły przekrojowe, które powstają w palach pod wpływem obciążeń zewnętrznych (tj. obciążenia poziomego i momentu zginającego).
Moduł sztywności poziomej gruntu Kx wyraża się wzorem:
natomiast graniczny odpór boczny gruntu Qxgr
Poszczególne składowe wzorów [1] i [2] opisano w artykule Sprężysto-plastyczna współpraca pali z gruntem. Należy zaznaczyć, że występujące w powyższych wzorach wartości współczynników n1 i n2 nie są stałe w obrębie fundamentu lecz zmieniają się w zależności od rozstawu sąsiednich pali.
Współczynnik n1 wyrażony jest wzorem:
Wartość współczynnika n2 wyznacza się w zależność od średnicy pala:
gdzie:
| D | średnica lub szerokość boku pala [m] |
| R1 | rozstaw osiowy pali w płaszczyźnie prostopadłej do kierunku działania obciążenia poziomego [m] |
| R2 | rozstaw osiowy pali w płaszczyźnie równoległej do kierunku działania obciążenia poziomego [m] |
| β | współczynnik zależny od liczby pali w rzędzie równoległym do kierunku działania obciążenia poziomego: β = 1,0 dla jednego rzędu pali β = 0,6 dla dwóch rzędów pali β = 0,5 dla trzech rzędów pali β = 0,45 dla czterech i więcej rzędów pali |
Schemat fundamentu palowego
Na potrzeby programu PaleKx opracowano schemat fundamentu palowego. Wyniki obliczeń sił przekrojowych prezentowane na schemacie fundamentu odwzorowują rzeczywisty fundament palowy. Obliczenia przeprowadzane są jednocześnie dla wszystkich pali schematu fundamentu oraz różnych kierunków działania obciążenia poziomego.
Poniższy przykładowy fundament podpory mostowej składa się z 29 sztuk pali. Skrajnym palom schematu nr 1÷3 i 7÷9 odpowiadają pojedyncze pale podpory mostowej natomiast wewnętrznym palom nr 4÷6 odpowiadają całe grupy pali.
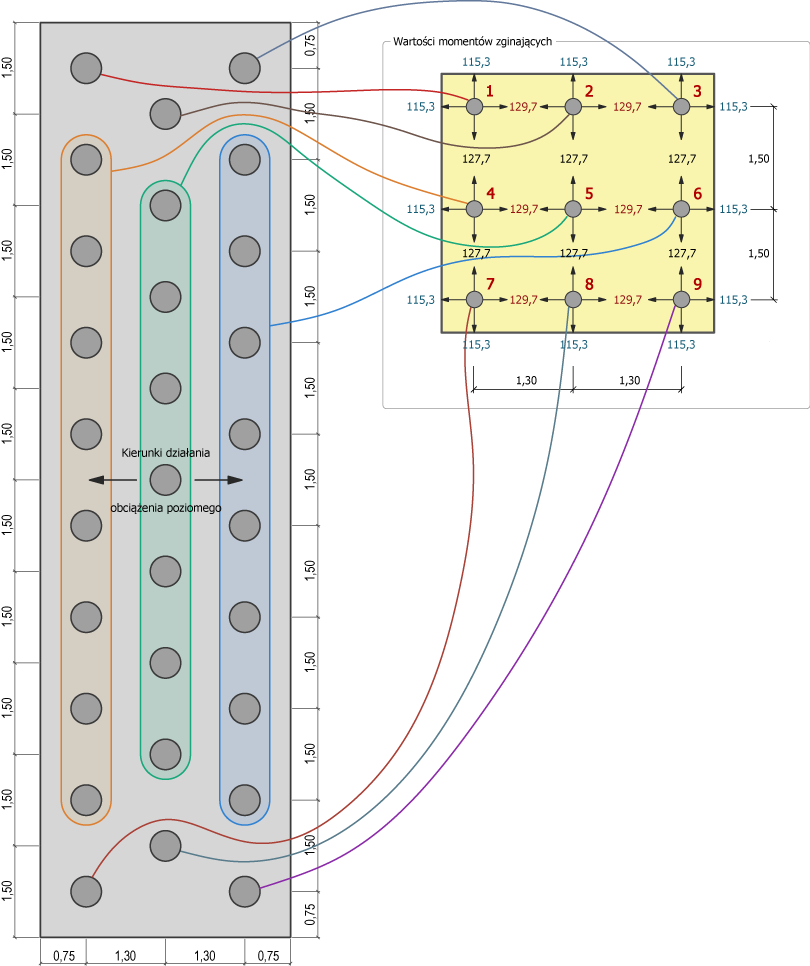
Obciążenie poziome równoległe do osi podłużnej mostu może działać w dwóch kierunkach. W zależności od kierunku obciążenia poziomego (< lub >) każdemu palowi odpowiadają dwie wartości maksymalnego momentu zginającego (115,3 kNm lub 129,7 kNm). Ponieważ obciążenie poziome działa na każdy pal naprzemiennie zatem wartość maksymalnego momentu zginającego na długości pala wynosi 129,7 kNm.

 Cart is empty
Cart is empty